# BitMap

在 java 中，一个 int 类型占 32 个 byte，我们用一个 int 数组来表示时未 new int[32] ,总计占用内存 32*32bit, 现假如我们用 int 字节码的每一位表示一个数字的话，那么 32 个数字只需要一个 int 类型所占内存空间大小就够了，这样在大数据量的情况下会节省很多内存。

具体思路：

1 个 int 占 4 字节即 4*8=32 位，那么我们只需要申请一个 int 数组长度为 int tmp[1+N/32] 即可存储完这些数据，其中N代表要进行查找的总数，tmp 中的每个元素在内存在占32位可以对应表示十进制数 0~31,所以可得到BitMap 表:

tmp[0]: 可表示 0~31

tmp[1]: 可表示 32~63

tmp[2]: 可表示 64~95

.......

那么接下来就看看十进制数如何转换为对应的bit位：

假设这 40 亿 int 数据为：6,3,8,32,36,......，那么具体的 BitMap 表示为：

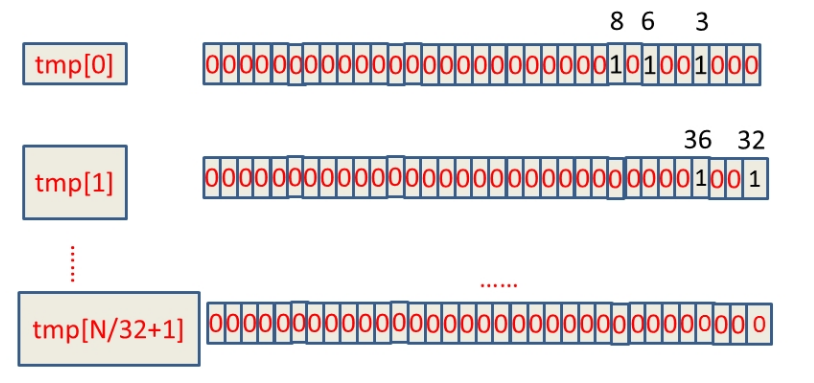
如何判断 int 数字在 tmp 数组的哪个下标，这个其实可以通过直接除以 32 取整数部分，例如：整数 8 除以 32 取整等于 0，那么 8 就在 tmp[0] 上。另外，我们如何知道了 8 在 tmp[0] 中的 32 个位中的哪个位，这种情况直接mod 上 32 就 ok，又如整数 8，在 tmp[0] 中的第 8 mod 上 32 等于 8，那么整数 8 就在 tmp[0] 中的第八个 bit 位（从右边数起）。

# BitMap应用

• 看个小场景 > 在 3 亿个整数中找出不重复的整数，限制内存不足以容纳 3 亿个整数。

对于这种场景我可以采用 2-BitMap 来解决，即为每个整数分配 2 bit，用不同的 0、1组合来标识特殊意思，如 00 表示此整数没有出现过，01 表示出现一次，11 表示出现过多次，就可以找出重复的整数了，其需要的内存空间是正常 BitMap 的2倍，为：3亿*2 / 8(字节B) / 1024(KB) / 1024(MB) = 71.5MB。

具体的过程如下：

扫描着 3 亿个整数，组 BitMap，先查看 BitMap 中的对应位置，如果 00 则变成 01，是 01 则变成 11，是 11 则保持不变，当将 3 亿个整数扫描完之后也就是说整个 BitMap 已经组装完毕。最后查看 BitMap 将对应位为11 的整数输出即可。

• 已知某个文件内包含一些电话号码，每个号码为 8 位数字，统计不同号码的个数。

8 位最多 99 999 999，大概需要 99 M 个 bit，大概 10 几m字节的内存即可。 （可以理解为从0-99 999 999的数字，每个数字对应一个Bit位，所以只需要 99M个Bit == 1.2MBytes，这样，就用了小小的 1.2M 左右的内存表示了所有的 8 位数的电话）

# BitMap问题

BitMap 的思想在面试的时候还是可以用来解决不少问题的，然后在很多系统中也都会用到，算是一种不错的解决问题的思路。

但是 BitMap 也有一些局限，因此会有其它一些基于 BitMap 的算法出现来解决这些问题。

• 数据碰撞。比如将字符串映射到 BitMap 的时候会有碰撞的问题，那就可以考虑用 Bloom Filter 来解决，Bloom Filter 使用多个 Hash 函数来减少冲突的概率。
• 数据稀疏。又比如要存入(10,8887983,93452134)这三个数据，我们需要建立一个 99999999 长度的 BitMap ，但是实际上只存了3个数据，这时候就有很大的空间浪费，碰到这种问题的话，可以通过引入 Roaring BitMap 来解决。

# 采用BitMap从 20 亿个int正整数中找出相同的数字

public class Test {
    //为了方便，假设数据是以数组的形式给我们的
    public static Set<Integer> test(int[] arr) {
        //用来把重复的数返回，存在Set里，这样避免返回重复的数。
        Set<Integer> output = new HashSet<>();
        BitSet bitSet = new BitSet(Integer.MAX_VALUE);
        int i = 0;
        while (i < arr.length) {
            int value = arr[i];
            //存在就添加到集合中
            if (bitSet.get(value)) {
                output.add(value);
            } else {
                bitSet.set(value, true);
            }
            i++;
        }
        return output;
    }
 
    public static void main(String[] args) {
        int[] t = {1,2,3,4,5,6,7,8,3,4};
        Set<Integer> t2 = test(t);
        System.out.println(t2);
    }
}