二叉树遍历
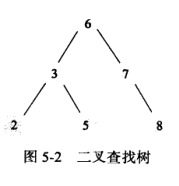
先序: 6 3 2 5 7 8
考察到一个节点后,即刻输出该节点的值,并继续遍历其左右子树。(根左右)
中序: 2 3 5 6 7 8
考察到一个节点后,将其暂存,遍历完左子树后,再输出该节点的值,然后遍历右子树。(左根右)
后序: 2 5 3 8 7 6
考察到一个节点后,将其暂存,遍历完左右子树后,再输出该节点的值。(左右根)
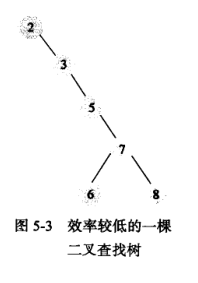
先序:2 3 5 7 6 8
中序:2 3 5 6 7 8
后序:6 8 7 5 3 2
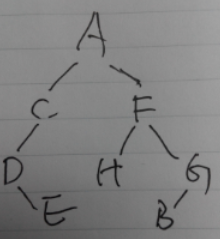
已知一个二叉树的前序遍历结果是(ACDEFHGB) ,中序遍历结果是(DECAHFBG),请问后续遍历结果是()。
A.HGFEDCBA
B.EDCHBGFA
C.BGFHEDCA
D.EDCBGHFA
E.BEGHDFCA
F.BGHFEDCA
平衡二叉树(红黑树)
像红黑树这样的平衡二叉树,无论如何插入元素,他都可以通过一些旋转的方法调整树的高度,使得整棵树的查询效率维持在O(logN)
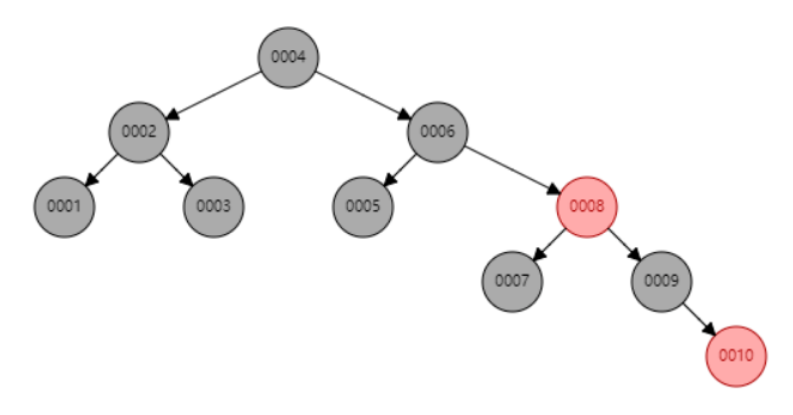
但是平衡二叉树的每个节点只有两个孩子节点,如果一张表的数据量特别大,整棵树的高度也会随之上升。一个千万级别的表如果用平衡二叉树作为索引的话,树高将会达到二十多层。这也就意味着做一次查询需要二十多次磁盘io,这是一个不小的开销。

B树和B+树
B树:一个节点可以存放N个孩子节点,这就完美解决了树高的问题,我们可以把B树称为平衡多叉树。
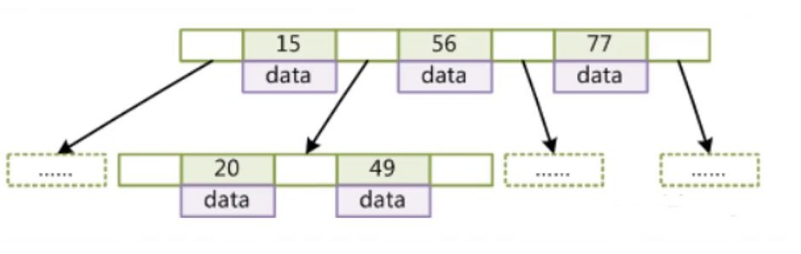
B+树:
- B+树的非叶子节点是不存储数据的,只存储索引,数据全部存储在叶子节点上。
- 叶子节点之间使用指针连接,提高区间访问效率。如果我们要进行范围查询,可以轻松通过B+树叶子节点之间的指针进行遍历,减少了不必要的磁盘 IO。
- 数据页都通过一个
双向链表来进行链接。
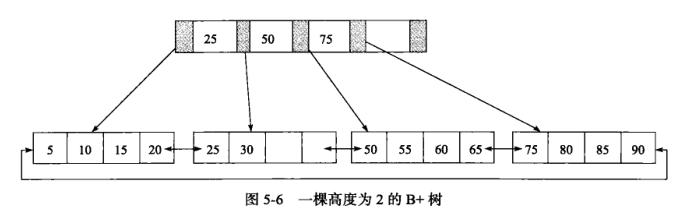
下面是一棵高度为 2 的 B+ 树,每页存放 4 条记录。上面一层叫 leaf page叶子页,下面的是index page索引页,插入删除操作都有可能对 leaf page 和 index page 进行拆分。 B+树的插入与删除
← BitMap
